[ad_1]
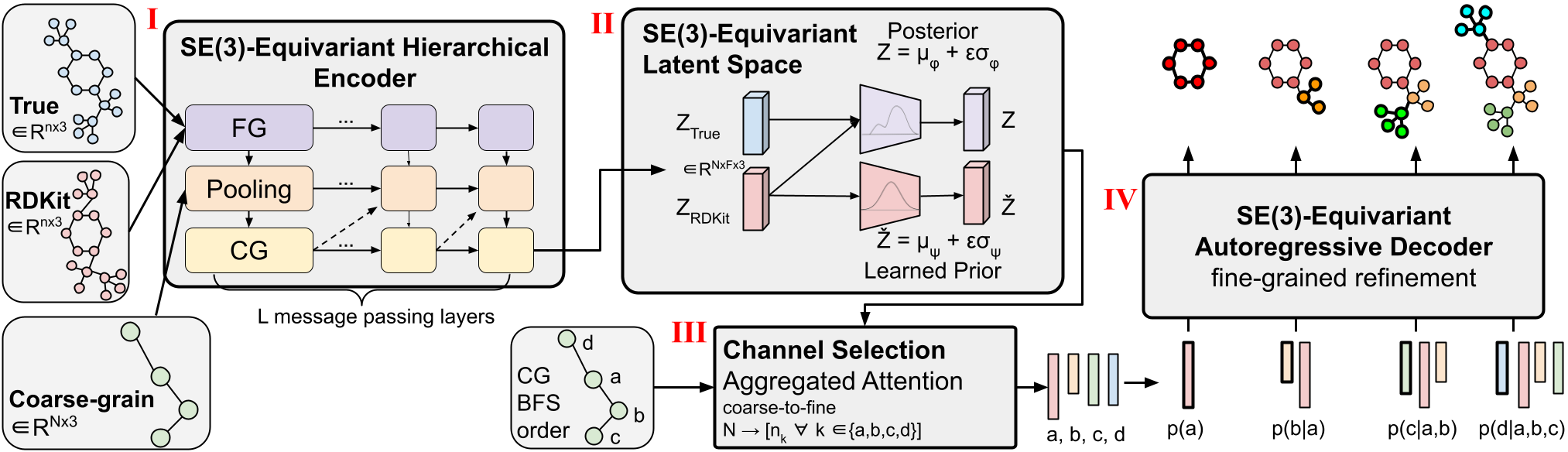
Figure 1: CoarsenConf architecture.
Molecular conformer generation is a fundamental task in computational chemistry. The goal is to predict stable low-energy 3D molecular structures, known as conformers, given a 2D molecule. Accurate molecular conformations are critical for a variety of applications that depend on precise spatial and geometric properties, including drug discovery and protein docking.
We present CoarsenConf, an SE(3)-equivariant hierarchical variational autoencoder (VAE) that combines information from fine-grained atomic coordinates into coarse-grained subgraph-level representations to generate an efficient autoregressive conformer.
background
Coarse grains reduce the dimensionality of the problem, allowing for conditional autoregressive generation rather than generating all coordinates independently as done in previous work. By conditioning directly on the 3D coordinates of previously generated subgraphs, our model generalizes better to chemically and spatially similar subgraphs. This mimics the process of basic molecular synthesis, where small functional units link together to form large drug-like molecules. Unlike previous methods, CoarsenConf generates low-energy conformers with the ability to directly model atomic coordinates, distances, and rotation angles.
The CoarsenConf architecture can be divided into the following components:
(m) Encoder $q_\phi(z| X, \mathcalR)$ takes the fine-grained (FG) ground truth $X$ , the RDKit approximate conformer $\mathcalR$ , and the coarse-grained (CG) ) conformer $\mathcalC $ as input (extracted from $X$ and a predefined CG strategy) and outputs a variable-length equivariant CG representation via equivariant message transfer and point convolutions.
(II) Equivariance MLP is used to study the mean and log variance of both the prior and prior distributions.
(III) The posterior (training) or anterior (inference) is sampled and fed to the channel selection module, where the attention layer is used to learn the optimal path from the CG to the FG structure.
(IV) Given the FG latent vector and the RDKit approximation, the decoder $p_\theta(X |\mathcalR, z)$ learns to recover the low-energy FG structure by sending an autoregressive equivariance message. The entire model can be trained end-to-end by optimizing the KL divergence of the latent distribution and reconstructing the error of the generated conformers.
MCG task formalism
We formulate the molecular conformer generation (MCG) task as modeling the conditional distribution $p(X|\mathcalR)$ , where $\mathcalR$ is the estimated conformer generated by RDKit and $X$ is the optimal one. low energy conformer(s). RDKit, a commonly used cheminformatics library, uses an inexpensive distance geometry-based algorithm followed by inexpensive physics-based optimization to achieve reasonable conformational approximations.
Coarse grained
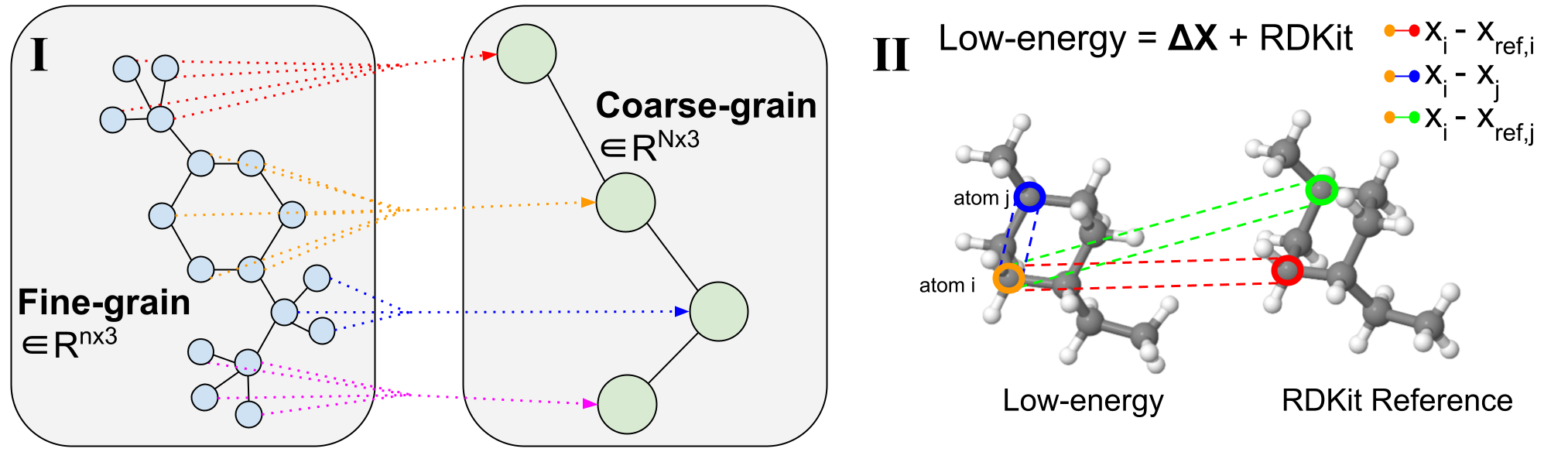
Figure 2: Coarse-grained process.
(m) An example of coarse grains of variable length. The fine-grained molecules are divided along the rotational bonds that define the rotational angles. They are then coarse-grained to reduce the dimensionality and learn subgraph-level latent distributions. (II) 3D conformer visualization. Specific atom pairs are marked for decoder message passing operations.
Molecular coarse-grained simplifies the representation of a molecule in its original structure by grouping fine-grained (FG) atoms into individual coarse-grained (CG) beads based on $\mathcalB$ rule-based mappings, as shown in Figure 2. (რ). Coarse-graining has been widely used in protein and molecular design, and similarly fragment-level or subgraph-level generation has proven to be very valuable in a variety of 2D molecular design tasks. Subdividing generative problems into smaller parts is an approach that can be used for several 3D molecule problems and provides a natural dimensionality reduction to allow working with large complex systems.
We note that compared to previous works that focus on fixed-length CG strategies, where each molecule is represented by a fixed resolution of $N$ CG beads, our method uses variable-length CG for its flexibility and ability to support coarse selection. grain technique. This means that a single CoarsenConf model can generalize to any coarse-grained resolution because the input molecules can map to any number of CG beads. In our case, the atoms consisting of each connected component resulting from the breaking of all rotating bonds dissolve into a single bead. In the CG procedure, this choice forces the model to learn rotation angles as well as atomic coordinates and interatomic distances. In our experiments, we use GEOM-QM9 and GEOM-DRUGS, which have an average of 11 atoms and 3 CG beads, and 44 atoms and 9 CG beads, respectively.
SE(3)-equivariance
A key aspect when working with 3D structures is to maintain appropriate equivariance. Three-dimensional molecules are equivariant in terms of rotation and translation, or SE(3)-equivariance. We implement SE(3)-equivariance in the CoarsenConf encoder, decoder, and hidden space of our probabilistic model. As a result, $p(X | \mathcalR)$ remains invariant for any rototranslation of the assumed conformer of $\mathcalR$ . Furthermore, if $\mathcalR$ is rotated clockwise by 90°, we expect $X$ to be optimally rotated the same way. For an in-depth explanation and discussion of equivariance-preserving methods, please see the full paper.
total attention
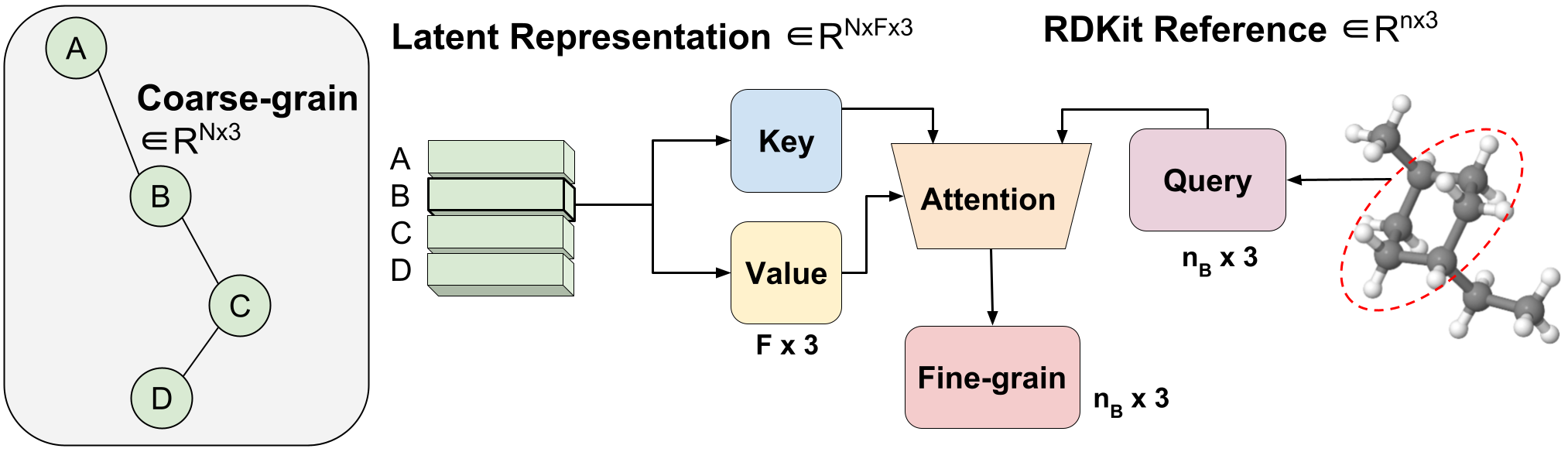
Figure 3: Variable-length coarse-to-fine mapping via aggregated attention.
We present a method we call aggregated attention to learn an optimal variable-length mapping from latent CG representations to FG coordinates. This is a variable-length operation, since a single molecule with $n$ atoms can fix on any number of $N$ CG beads (each bead is represented by a single latent vector). One CG bead latent vector $Z_B$ $\in R^F \times 3$ is used as key and value by one head attention operation with built-in dimension three to match the x, y, z coordinates. The query vector is a subset of the RDKit conformer corresponding to the bead $B$ $\in R^ n_B \times 3$ , where $n_B$ is of variable length because we know how many FG atoms are conforming. on a certain CG bead. By focusing attention, we effectively learn the optimal combination of hidden features for FG reconstruction. We call this combined attention because it combines the 3D segments of FG information to form our hidden query. Aggregated attention is responsible for efficient translation from latent CG representations to viable FG coordinates (Figure 1(III)).
model
CoarsenConf is a hierarchical VAE with SE(3)-equivariant encoder and decoder. The encoder works with SE(3) invariant atomistic features $h \in R^n \times D$ and SE(3)-equivariant atomistic coordinates $x \in R^n \times 3$ . One coding layer consists of three modules: fine-grained, combined and coarse-grained. The complete equations for each module can be found in the full paper. The encoder produces the final equivalent CG tensor $Z \in R^N \times F \times 3$ , where $N$ is the number of beads and F is the user-defined hidden size.
The role of the decoder is twofold. The first is to transform the latent coarse representation into FG space through a process we call channel selection that uses aggregated attention. The second is to refine the fine-grained representation autoregressively to generate the final low-energy coordinates (Figure 1 (IV)).
We emphasize that by coarse-graining the rotation angles, our model learns the optimal rotation angles without supervision, since the conditional input to the decoder is not smoothed. CoarsenConf ensures that each subsequent generated subgraph is correctly rotated to achieve low coordinate and distance errors.
Experimental results
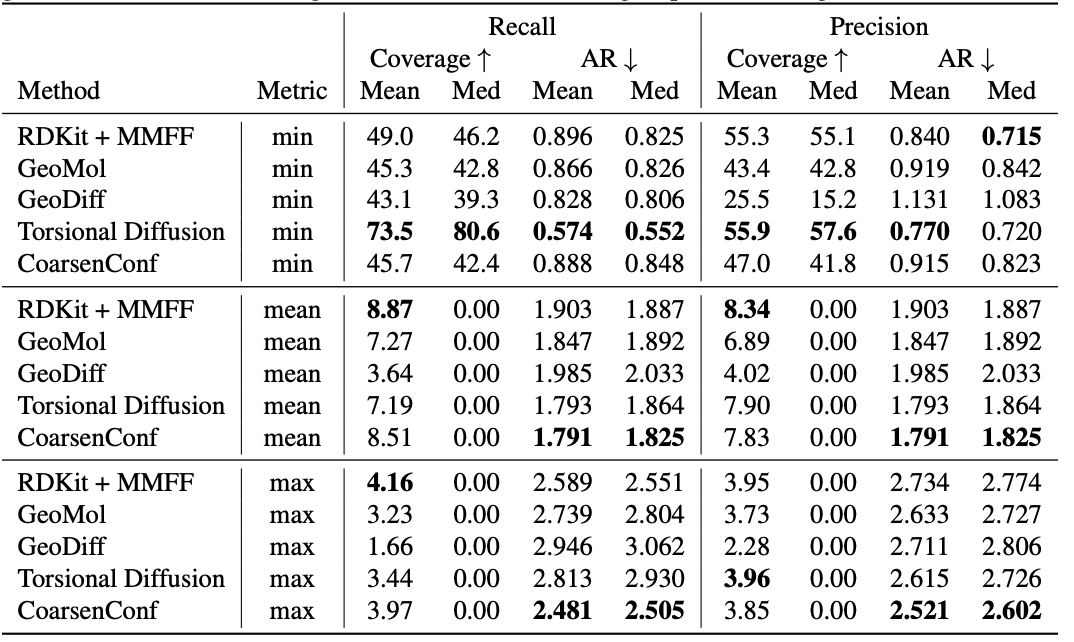
Table 1: quality of the generated conformer ensembles for the GEOM-DRUGS test set ( $\delta=0.75Å$ ) in terms of coverage (%) and mean RMSD ($Å$ ). CoarsenConf (5 epochs) was limited to 7.3% of the data used by Torsional Diffusion (250 epochs), a low computational and data limited mode example.
The average error (AR) is a basic metric that measures the average RMSD for the generated molecules of the corresponding test set. Coverage measures the percentage of molecules that can be produced within a specific error threshold ( $\delta$ ). We introduce the mean and max metrics to better estimate robust generation and avoid min metric selection bias. We emphasize that the min metric provides non-material results, because if the optimal conformer is not known a priori, there is no way to know which conformer generated 2L is the best for a single molecule. Table 1 shows that CoarsenConf produces the lowest average and worst errors for the entire test set of DRUGS molecules. We also show that RDKit, with low-cost physics-based optimization (MMFF), achieves better coverage than most deep learning-based methods. For official metrics definitions and further discussion, please see the full paper linked below.
For more information about CoarsenConf, read the paper on arXiv.
BibTex
If CoarsenConf inspires your work, please consider citing it:
@articlereidenbach2023coarsenconf,
title=CoarsenConf: Equivariant Coarsening with Aggregated Attention for Molecular Conformer Generation,
author=Danny Reidenbach and Aditi S. Krishnapriyan,
journal=arXiv preprint arXiv:2306.14852,
year=2023,
[ad_2]
Source link

