Why do policy gradient methods work so well in Cooperative MARL? Evidence from policy representation

In Cooperative Multi-Agent Reinforcement (MARL), due to on politics In nature, policy gradient (PG) methods are generally considered to be less efficient than value decomposition (VD) methods, which outside politics. However, some recent empirical studies have shown that with proper input representation and hyper-parameter tuning, multi-agent PG can achieve remarkably strong performance compared to policy-free VD methods.

Why might PG methods work so well? In this post, we present a specific analysis to show that in certain scenarios, such as an environment with a highly multimodal reward landscape, VD can be problematic and lead to undesirable outcomes. In contrast, PG methods with individual policies can converge to optimal policies in these cases. In addition, PG methods with autoregressive (AR) policies can learn multimodal policies.

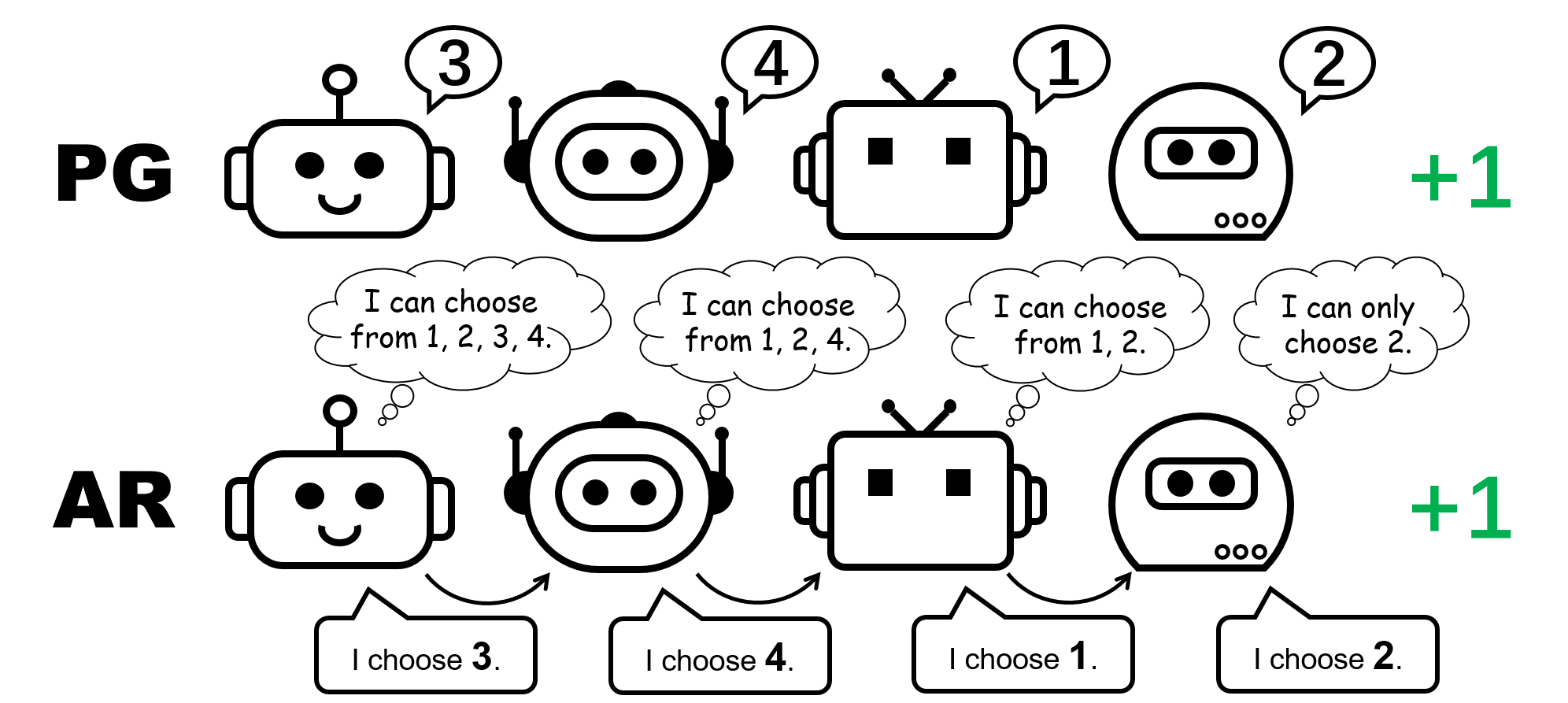
Figure 1: Representation of different policies for a 4-player permutation game.

CTDE in Cooperative MARL: VD and PG methods

Centralized Training and Decentralized Execution (CTDE) is a popular framework in cooperative MARL. These levers global Information for more effective training while maintaining individual policy representation during testing. CTDE can be implemented via value decomposition (VD) or policy gradient (PG), resulting in two different types of algorithms.

VD methods learn local Q networks and a mixing function that combines local Q networks with a global Q function. The mixing function is typically performed to satisfy the individual-global-max (IGM) principle, which guarantees that the joint optimal action can be computed by greedily choosing the locally optimal action for each agent.

In contrast, PG methods directly apply the policy gradient to learn individual policies and a centralized cost function for each agent. The value function takes as its input the global state (e.g., MAPPO) or the concatenation of all local observations (e.g., MADDPG) to estimate the exact global value.

The permutation game: A simple counterexample where VD fails

We begin our analysis by considering a stateless cooperative game, namely a permutation game. In an $N$ -player permutation game, each agent can issue $N$ actions $ 1,\ldots, N $ . Agents receive a reward of $+1$ if their actions are mutually exclusive, that is, the joint action is a permutation greater than $1, \ldots, N$; Otherwise, they will receive a $0 reward. Note that there are $N!$ symmetric optimal strategies in this game.

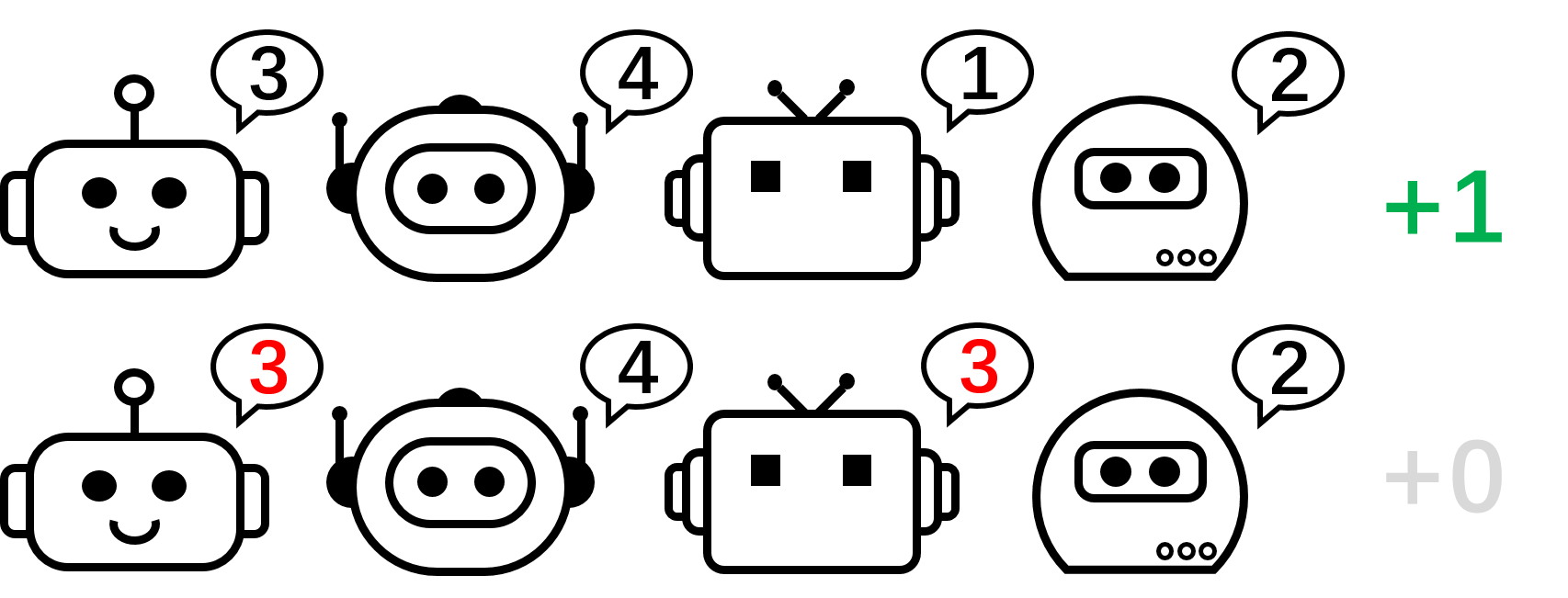
Figure 2: A 4-player permutation game.

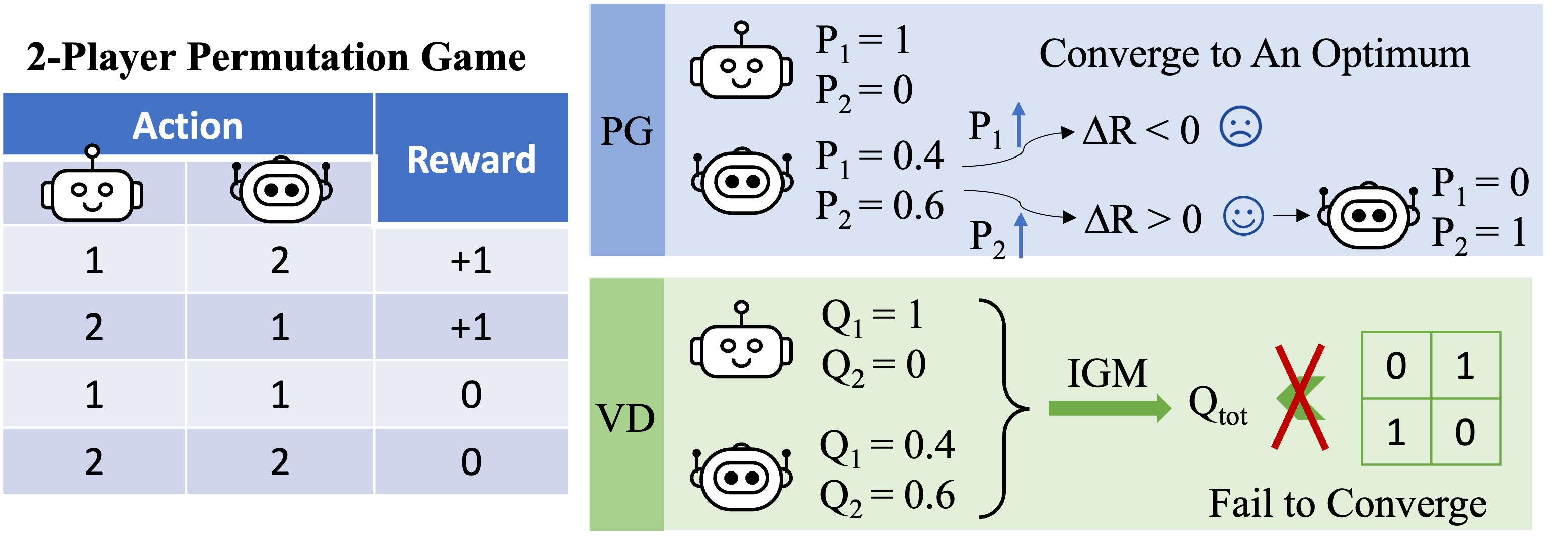
Figure 3: High-level intuition about why VD fails in a 2-player permutation game.

Let’s now focus on the 2-player permutation game and apply VD to the game. In this unnamed setting, we use $Q_1$ and $Q_2$ to denote the local Q-functions and use $Q_\textrmtot$ to denote the global Q-function. The IGM principle requires this

\[\arg\max_a^1,a^2Q_\textrmtot(a^1,a^2)=\\arg\max_a^1Q_1(a^1),\arg\max_a^2Q_2(a^2)\.\]

We argue that VD cannot represent the payoff of a 2-player permutation game with contradictions. If VD methods could produce returns, we would

\[Q_\textrmtot(1, 2)=Q_\textrmtot(2,1)=1\quad \textand\quad Q_\textrmtot(1, 1)=Q_\textrmtot(2,2)=0.\]

If any of these two agents have different local Q values ​​(eg, $Q_1(1)> Q_1(2)$), we have $\arg\max_a^1Q_1(a^1)=1$. Then according to the IGM principle, any Optimal joint action

\[(a^1\star,a^2\star)=\arg\max_a^1,a^2Q_\textrmtot(a^1,a^2)=\\arg\max_a^1Q_1(a^1),\arg\max_a^2Q_2(a^2)\\]

satisfies $a^1\star=1$ and $a^1\star\neq 2$, so the joint action $(a^1,a^2)=(2,1)$ is sub-optimal , that is, $Q_\textrmtot(2,1)<1$.

Otherwise, if $Q_1(1)=Q_1(2)$ and $Q_2(1)=Q_2(2)$, then

\[Q_\textrmtot(1, 1)=Q_\textrmtot(2,2)=Q_\textrmtot(1, 2)=Q_\textrmtot(2,1).\]

As a result, the cost decomposition cannot represent the payoff matrix of a 2-player permutation game.

What about PG methods? An individual policy may indeed represent an optimal policy for a permutation game. Moreover, stochastic gradient descent guarantees that PG will converge to one of these optima under mild assumptions. This suggests that, although PG methods are less popular in MARL than VD methods, they may be preferred in certain cases common in the real world, such as games with multiple strategy modes.

We also note that in a permutation game, to represent an optimal joint policy, each agent must choose different actions. Therefore, a successful PG implementation must ensure that policies are agent-specific. This can be done using an individual policy with non-shared parameters (referred to as PG-Ind in our paper), or using an agent-ID conditional policy (PG-ID).

PG outperforms existing VD methods on popular MARL testbeds

Beyond the simple illustrative example of the permutation game, we extend our study to popular and more realistic MARL benchmarks. In addition to the StarCraft Multi-Agent Challenge (SMAC), where the effectiveness of PG and agent-driven policy input is proven, we show new results in Google Research Football (GRF) and the multiplayer Hanabi Challenge.

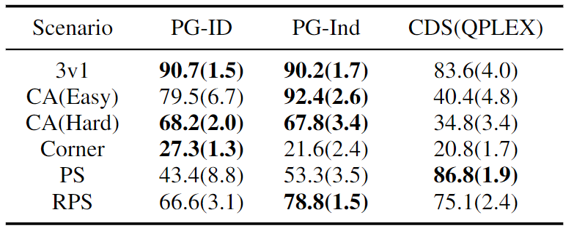
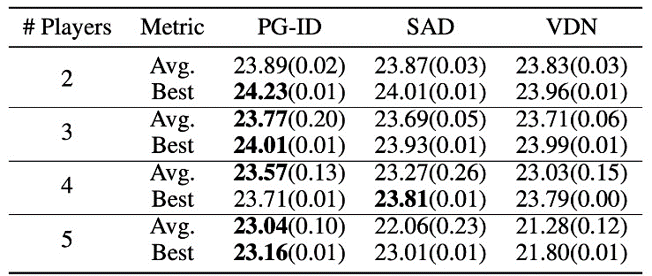
Figure 4: (left) gain rates of PG methods on GRF; (Right) Best and average evaluation scores on Hanabi-Full.

PG methods in GRF outperform the modern VD baseline (CDS) in 5 scenarios. Interestingly, we also observe that the individual policy (PG-Ind) without parameter sharing achieves comparable, sometimes higher, profit rates compared to the agent-specific policy (PG-ID) in all 5 scenarios. We evaluate PG-ID in a full-scale Hanabi game with different numbers of players (2-5 players) and compare them to SAD, a robust variant of policy-free Q-learning in Hanabi, and Value Decomposition Networks (VDN). As can be seen from the table above, PG-ID can produce results comparable to or better than the best and average rewards achieved by SAD and VDN with different numbers of players using the same number of environmental steps.

Beyond the highest reward: Learning multimodal behavior through auto-regressive policy modeling

In addition to learning about higher honors, we also learn how to learn multi-modal policies at Cooperative MARL. Back to the permutation game. Although we have proven that PG can efficiently learn the optimal policy, the strategy mode it finally reaches can be highly dependent on the initialization of the policy. Thus, a natural question would be:

Can we learn a single policy that can cover all optimal regimes?

In the decentralized PG formulation, the factorized representation of the joint policy can represent only one specific mode. Therefore, we propose an enhanced way to parameterize policies for stronger expressiveness—autoregressive (AR) policies.

Figure 5: Comparison between individual policy (PG) and auto-regressive policy (AR) in a 4-player permutation game.

Formally, we transform the joint policy of $n$ agents into the form

\[\pi(\mathbfa \mid \mathbfo) \approx \prod_i=1^n \pi_\theta^i \left( a^i\mid o^i,a^1,\ldots,a^i-1 \right),\]

where the action taken by agent $i$ depends on its own observation $o_i$ and all actions from previous agents $1,\dots,i-1$. Autoregressive factorization can represent any Joint policies in a centralized MDP. The only Each agent’s policy change is an input dimension that is slightly expanded to include previous actions; And the output dimension of each agent’s policy remains unchanged.

With such minimal parameterization overhead, the AR policy substantially improves the representation power of PG methods. We note that PG with AR policy (PG-AR) can simultaneously represent all optimal policy regimes in a permutation game.

Figure: Heatmaps of actions for policies learned by PG-Ind (left) and PG-AR (middle) and heatmap of rewards (right); While PG-Ind only encounters a specific mode in a 4-player permutation game, PG-AR successfully detects all optimal modes.

In more complex environments, including SMAC and GRF, PG-AR can learn interesting emergent behaviors that require strong intra-agent coordination, which PG-Ind may never learn.

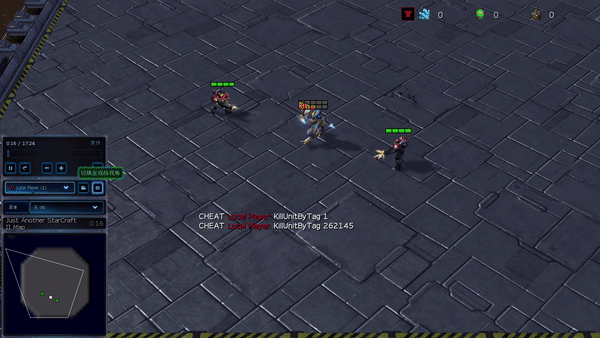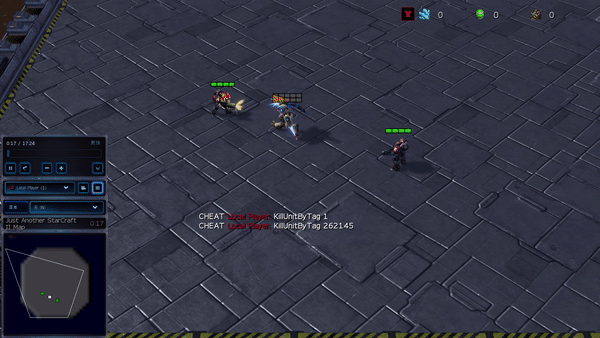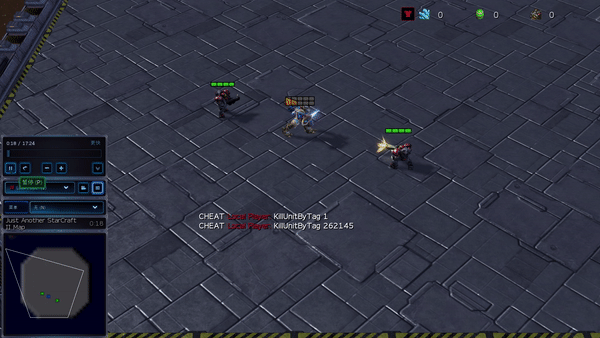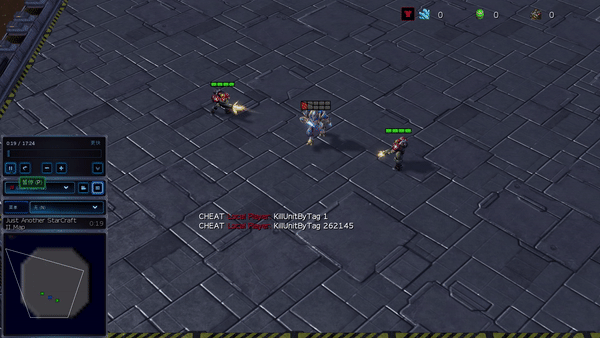
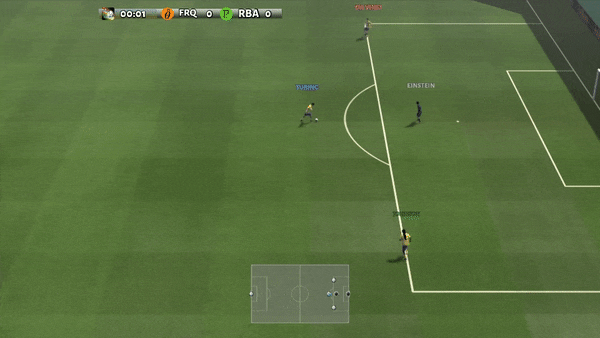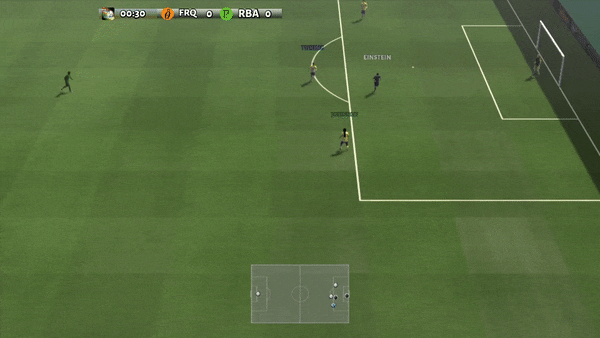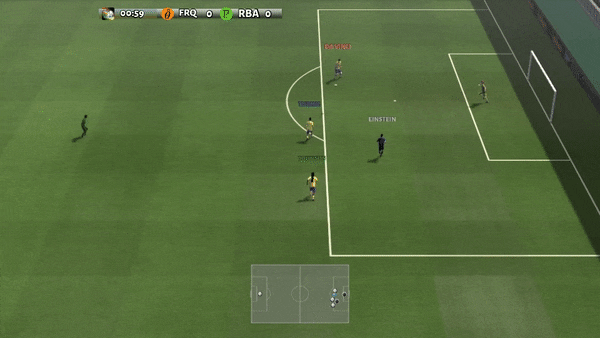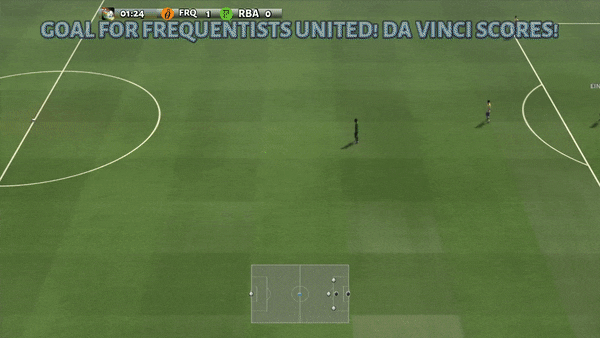
Figure 6: (Left) Emergent behavior induced by PG-AR in SMAC and GRF. In SMAC’s 2m_vs_1z map, Marines take turns standing and attacking while making sure there is only one attacking Marine in each phase; (Right) In the GRF scenario of Academy_3_vs_1_with_meeper, the agents learn to behave in a “tiki-taka” style: each player keeps passing the ball to his teammates.

Discussions and presenters

In this post, we provide a concrete analysis of VD and PG methods in cooperative MARL. First, we reveal the expressivity limitation of popular VD methods, showing that they cannot represent optimal policies even in a simple permutation game. In contrast, we show that PG methods are more pronounced. We empirically test the expressiveness superiority of PG on popular MARL testbeds including SMAC, GRF, and Hanabi Challenge. We hope that the insights gained from this work can be useful to the community towards more general and more robust collaborative MARL algorithms in the future.

This post is based on our paper: A Review of Some Common Practices in Cooperative Multi-Agent Reinforcement Learning (paper, website).