[ad_1]
Deep neural networks have produced technological marvels, from voice recognition to driving cars to protein engineering, but their design and use are still decidedly unprincipled. Developing tools and methods to guide this process is one of the main challenges of deep learning theory. In Reverse Engineering a Neural Tangent Kernel, we propose a paradigm for bringing some principle to the art of architecture design using recent theoretical advances: first design a good kernel function—often a much easier task—and then “reverse engineer” the kernel equivalence to translate the chosen kernel into a neural network. Our main theoretical result allows the development of activation functions from first principles, and we use it to construct one activation function that mimics the performance of a deep \(\textrmReLU\) network with only one hidden layer and another that clearly outperforms deep \( \textrmReLU \) networks on the synthetic task.
Cores returned to networks. Fundamental work has developed formulas that map large neural networks to their corresponding cores. We obtain an inverse mapping that allows us to start from the desired core and transform it into a network architecture.
Neural network kernels
The field of deep learning theory has recently changed with the realization that deep neural networks are often analytically amenable to study. infinite width limit. Take the limit in a certain way and the network actually converges to a conventional kernel method using the “Neural Tangent Kernel” (NTK) architecture, or, if only the last layer is trained (ala random function models), its “Neural Network Gaussian Process” (NNGP) kernel. Like the central limit theorem, these wide network bounds are often surprisingly good approximations, even far from infinite width (often valid for hundreds or thousands of widths), providing excellent insights into the mysteries of deep learning.
From networks to cores and back again
Early work investigating this net-kernel correspondence gave formulas to go architecture that core: By describing the architecture (eg depth and activation function), they give you two cores of the network. This allowed great insight into the optimization and generalization of various interesting architectures. However, if our goal is not only to understand the existing architecture, but also to design new condition, then we may rather have a map in the opposite direction: given a core If we want, we can find it architecture that gives us In this paper, we derive this inverse mapping for fully connected networks (FCNs), allowing us to construct simple networks in a principled way by (a) locating a desired kernel and (b) devising an activation function that yields it.
To understand why this makes sense, let’s first imagine NTK. Consider the NTK of a wide FCN \(K(x_1,x_2)\) on two input vectors \(x_1\) and \(x_2\) (which we assume to be normalized to the same length for simplicity). For FCN, this is the core rotation-invariant in the sense that \(K(x_1,x_2) = K(c)\), where \(c\) is the cosine of the angle between the inputs. Since \(K(c)\) is a scalar function of a scalar argument, we can simply plot it. fig. 2 shows a four hidden layer (4HL) \(\textrmReLU\) FCN NTK.
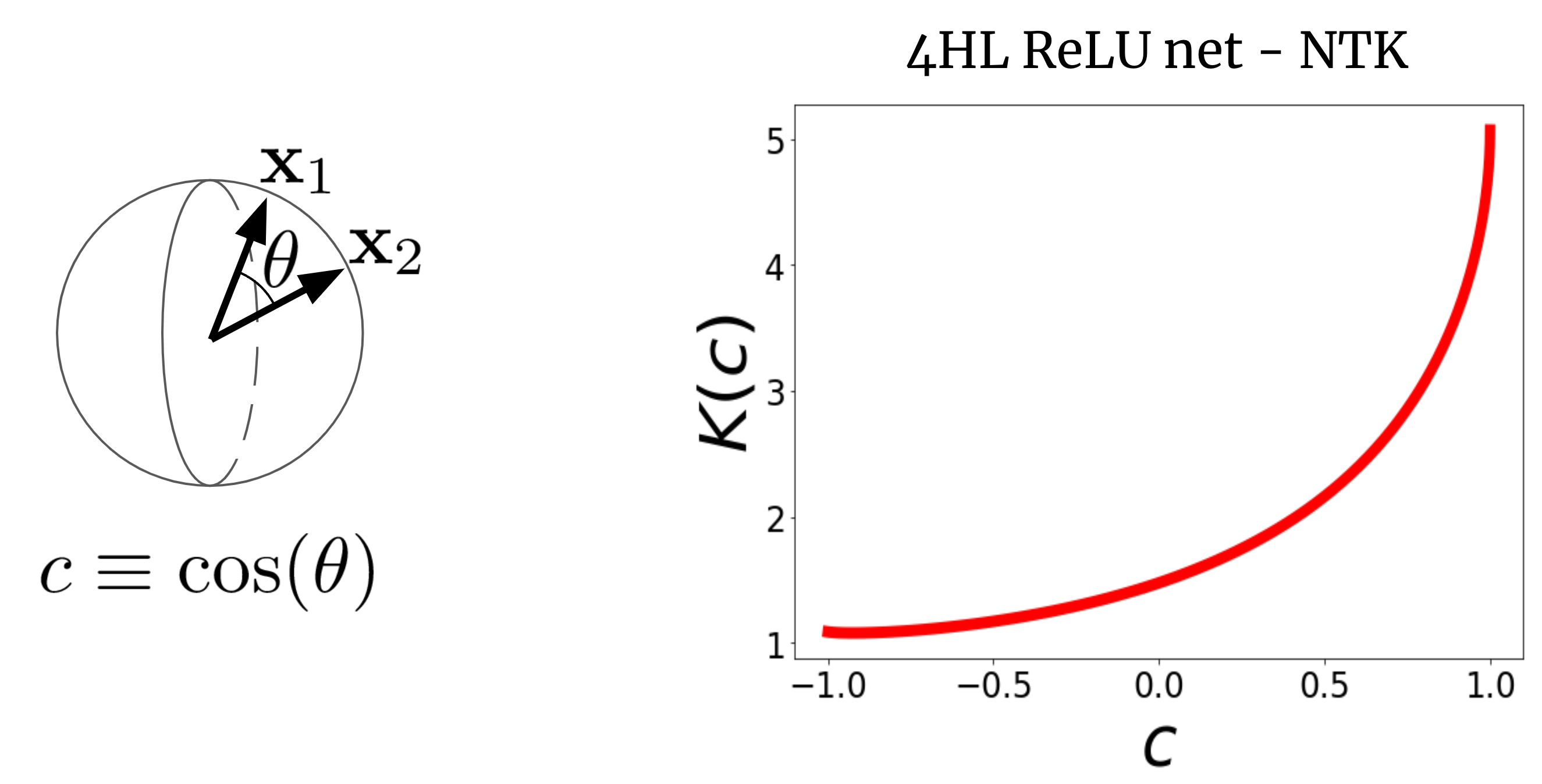
Fig. 2. NTK of 4HL $\textrmReLU$ FCN as a cosine function between two input vectors $x_1$ and $x_2$ .
This plot actually contains a lot of information about relevant wide net learning behavior! Monotonic growth means that this kernel expects closer points to have more correlated function values. A sharp increase at the bottom tells us that the correlation length is not too large and it can fit complex functions. The differentiable derivative at \(c=1\) tells us the smoothness of the function we expect to obtain. it’s important, None of these facts are apparent from the \(\textrmReLU(z)\) diagram! We argue that if we want to understand the effect of choosing the activation function \(\phi\), then the resulting NTK is actually more informative than \(\phi\) itself. Thus, it makes sense to design architectures in “kernel space” and then translate them to typical hyperparameters.
Activation function for all cores
Our main result is the “reverse engineering theorem”, which states:
Theme 1: For any kernel $K(c)$, we can construct an activation function $\tilde\phi$ such that the embedding One hidden layer FCN, its infinite width NTK or NNGP kernel is $K(c)$.
We give an explicit formula for \(\tilde\phi\) in terms of Hermite polynomials (although in practice we use a different functional form for training reasons). Our proposed use of this result is that for problems with some known structure, it may sometimes be possible to write a good kernel and reverse-engineer it into a training network, with various advantages over pure kernel regression, such as computational efficiency and feature learning ability. As a proof of concept, we test this idea on synthetics The parity problem (ie, given a bit string, is the sum odd or even?), immediately produces an activation function that dramatically outperforms the \(\textReLU\) problem.
Is one hidden layer all you need?
Here is another amazing use of our result. The kernel curve above is for a 4HL \(\textrmReLU\) FCN, but I have argued that we can achieve any kernel, including one, with only one hidden layer. This means that we can use a new activation function \(\tilde\phi\) that gives this “deep” NTK Shallow web! fig. 3 illustrates this experiment.
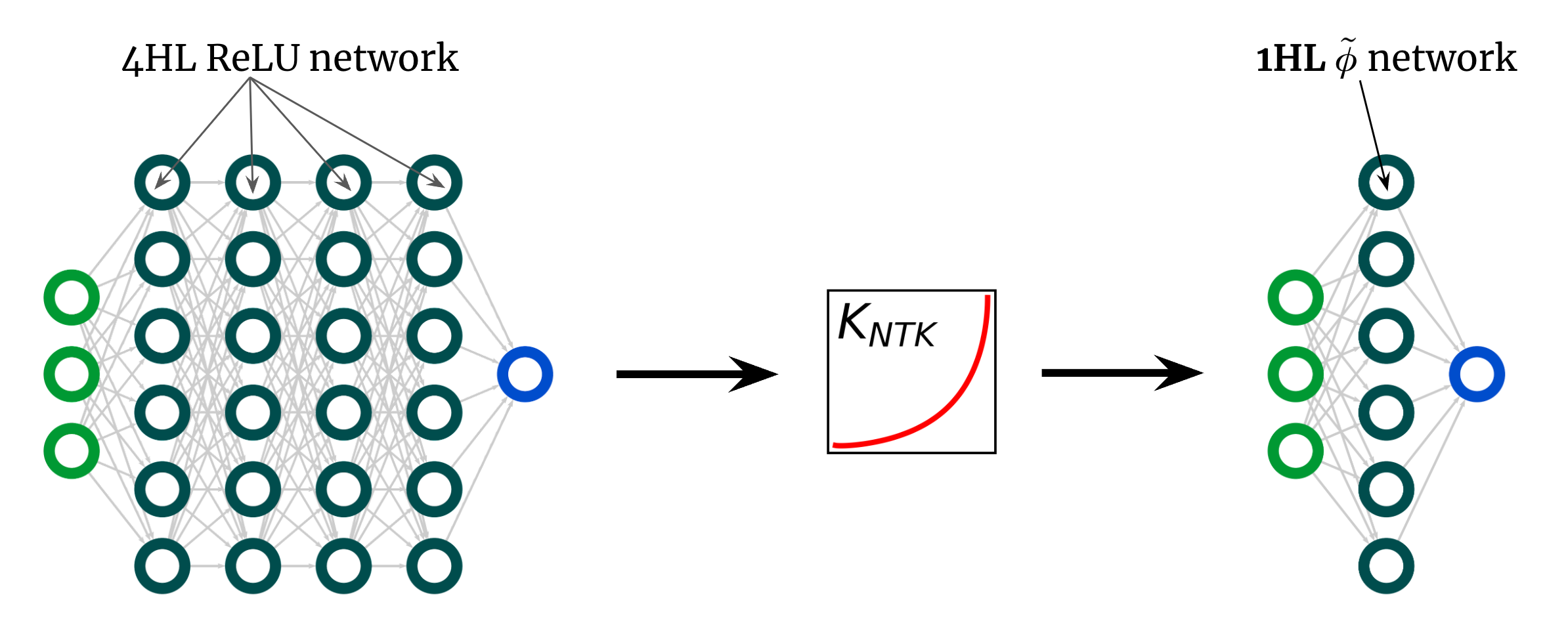
Fig. 3. Superficiation of a deep $\textrmReLU$ FCN with an engineered activation $\tilde\phi$ function in a 1HL FCN.
Surprisingly, this “shallow” actually works. fig. The left subplot of Fig. 4 shows the “mimic” activation function \(\tilde\phi\) which yields practically the same NTK as the deep \(\textrmReLU\) FCN. The right plots then show the train + test loss + accuracy traces for the three FCNs on the standard tableau problem from the UCI data set. Note that although shallow and deep ReLU networks have very different behavior, our engineered shallow mimic network tracks the deep network almost exactly!
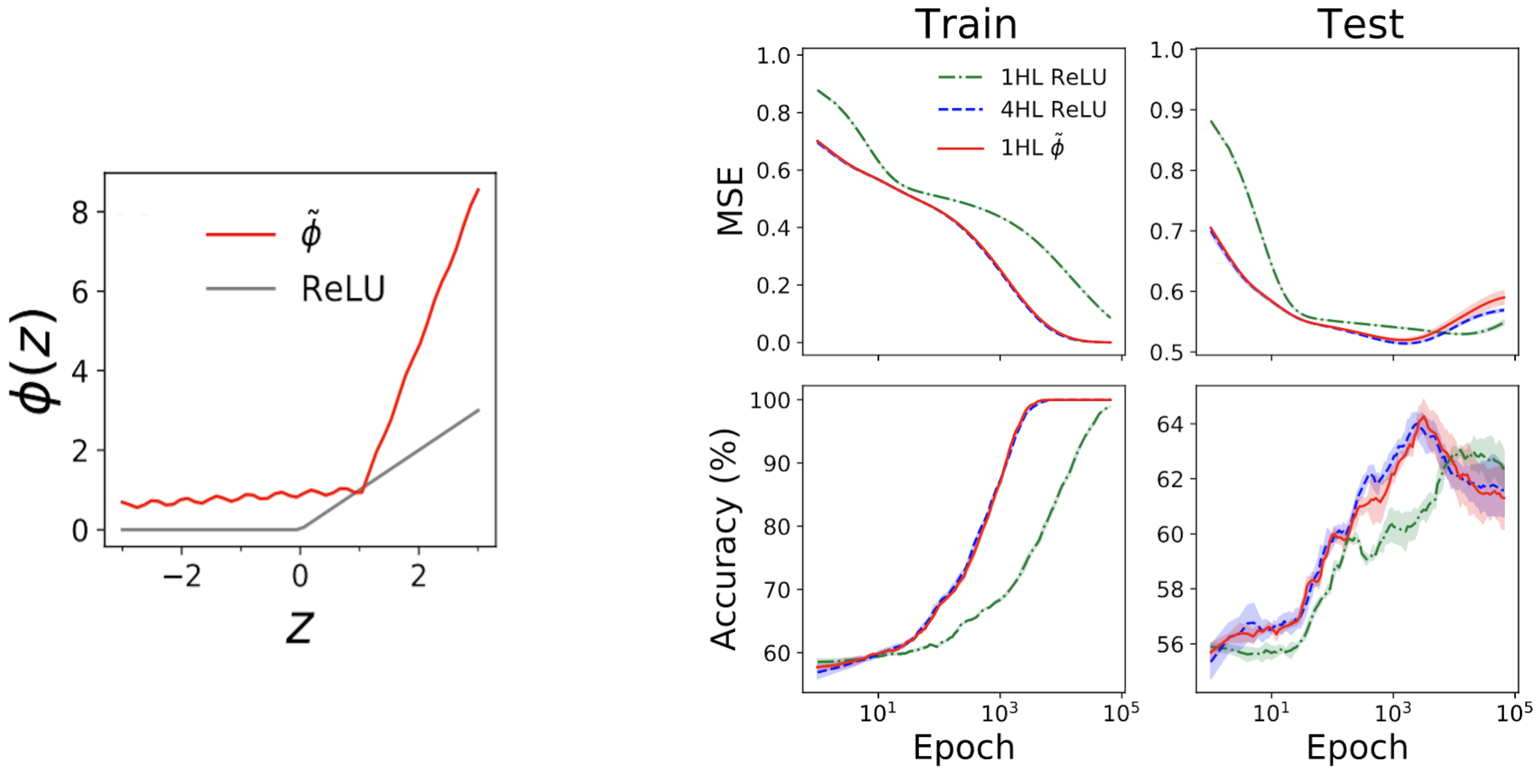
Fig. 4. Left panel: our engineered “mimic” activation function, plotted with ReLU for comparison. Right panels: performance traces for 1HL ReLU, 4HL ReLU and 1HL simulated FCNs trained on the UCI database. Note the close match between the 4HL ReLU and 1HL mimic networks.
This is interesting from an engineering perspective because the shallow network uses fewer parameters than the deep network to achieve the same performance. It is also interesting from a theoretical point of view because it raises fundamental questions about the value of depth. A common belief in deep learning is that deeper is not only better, but qualitatively different: that deep networks can effectively learn features that shallow networks simply cannot. Our shallowness result suggests that, at least for FCNs, this is not true: if we know what we’re doing, then depth doesn’t buy us anything.
conclusion
This work comes with a number of caveats. The biggest one is that our results only apply to FCNs, which are rarely contemporaneous. However, work on convolutional NTKs is progressing rapidly, and we believe that this paradigm of designing networks with kernel design is ripe for some form of extension to these structured architectures.
Theoretical work has so far provided relatively few tools for practical deep learning theorists. Our goal is for this to be a modest step in that direction. Even without science guiding their design, neural networks have already worked wonders. Just imagine what we’ll be able to do with them once we finally have them.
This post is based on the paper “Reverse Engineering the Neural Tangent Kernel”, a joint work with Sajjant Anand and Mike Dewey. We provide code to reproduce all our results. We will be happy to address your questions or comments.
[ad_2]
Source link

