More tricks to improve the performance of the CIFAR-10 classifier

Some time ago I wrote a post about tricks to improve the performance of the CIFAR-10 classifier, based on what I learned from a New York University deep learning course taught by Jan Le Kuhn and Alfredo Canzian. The tricks I covered were conveniently placed on one slide in one of the lectures. Soon after, I heard about a few other tricks that had been mentioned in the past, so I figured it would be interesting to try them out as well to see how well they worked. This is the topic of this blog post.

As before, the tricks themselves aren’t radically new or anything, my interest in implementing these techniques is as much about learning how to do them using Pytorch as it is about their effectiveness in a classification task. The task is relatively simple – the CIFAR-10 dataset contains about 1000 (800 training and 200 test) low-resolution 32×32 RBG images, and the task is to classify them into one of 10 different classes. The network we use is adapted from the CNN described in the Tensorflow CNN tutorial.

We start with a base network identical to the one described in the Tensorflow CNN tutorial. We train the network using the training set and evaluate the trained network’s classification accuracy (micro-F1 score) on the test set. All models were trained for 10 epochs using the Adam optimizer. Here are the different scenarios I tried.

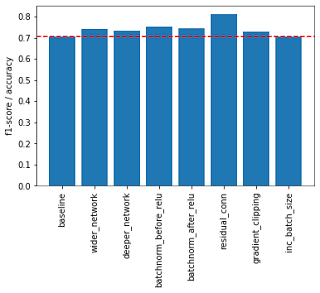
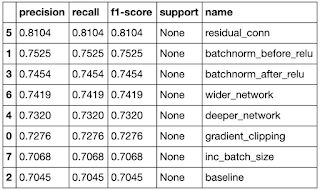
1. basic — This is a CNN with three layers of convolutions and max pooling, followed by a two-layer classification chapter. It uses the Coss Entropy loss function and the Adam optimizer with a fixed learning rate of 1e-3. The size of the input filter is 3 (RGB images), and the convolution layers create 32, 64, and 64 channels, respectively. The resulting tensor is flattened and passed through two linear layers to calculate the softmax likelihood for each of the 10 classes. The number of training parameters in this network is 122,570 and it achieves an accuracy score of 0.705.
2. Wide network — The last layer size of the trailing or dense part of the network has been expanded from 64 to 512, the number of trained parameters to 586250, and the score to 0.742.
3. A deeper network — Similar to the previous approach, the number of layers in the dense part of the network has been increased from one layer of size 64 to two layers (512, 256). As the previous approach, this increased the number of training parameters to 715,018 and a score of 0.732.
4. Series normalization (to ReLU) — This trick adds a Batch Normalization layer after each convolution layer. There is some confusion about whether to install BatchNorm before or after ReLU activation, so I tried both ways. In this configuration, the BatchNorm layer is placed before the ReLU activation, ie, each convolution block looks like (Conv2d → BatchNorm2d → ReLU → MaxPool2d). The BatchNorm layer functions as a regularizer and increases the number of training parameters slightly to 122,890 and gives a score of 0.752. Between the two setups (this and one), this seems to be the better setup based on my results.
5. Series normalization (after ReLU) — This setup is identical to the previous one, except that the BatchNorm layer is placed after ReLU, so each convolution block now looks like this (Conv2d → ReLU → BatchNorm2d → MaxPool2d). This configuration gives a score of 0.745, which is less than the score of the previous setup.
6. residual connection — This approach involves switching each Convolution block (Conv2d → ReLU → MaxPool2d) with a basic ResNet block consisting of two Convolution layers with a shortcut residual connection, followed by ReLU and MaxPool. This increases the number of training parameters to 212,714, which is much more modest than the wider and deeper network approaches, but with a much higher score increase (the highest among all approaches tried) to 0.810.
7. Gradient clipping — Gradient Clipping is more commonly used with recurrent networks, but serves a similar function as BatchNorm. It keeps the gradients from blowing up. It is used as a correction during the training cycle and does not create new trinable parameters. It yielded a much more modest gain of 0.728 points.
8. Increase batch size — Increasing the streak size from 64 to 128 did not significantly change the score, it increased from 0.705 to 0.707.

The code for these experiments is available in the notebook at the link below. It was run on a Colab (Google Colaboratory) (free) GPU instance. You can re-run the code in Colab by using the Open in Colab button at the top of the notebook.

The evaluation results for each different trick are summarized in the bar chart and table below. All strategies outperformed the baseline, but the best performer was the one using residual linkages, which outperformed the baseline by about 14 percentage points. Other notable performers were BatchNorm and its installation before ReLU activation performed better than after. The wider and deeper machining of the denser head also worked well to increase performance.

Another thing I looked at was the efficiency of the setting. Expanding and deepening the dense head layers resulted in the greatest increase in the number of training parameters, but did not lead to a corresponding increase in performance. On the other hand, adding Batchnorm increased performance with a small increase in the number of parameters. The residual coupling approach increased the number of parameters somewhat, but provided a much larger performance boost.

And that’s all I had for today. It was fun to use the dynamic nature of Pytorch to create relatively complex models without many more lines of code. I hope you found it useful.

Edit 2021-03-28: I had a bug in my notebook where I was creating an extra layer in the FCN head that I didn’t intend to do, so I fixed it and ran the results again, which gave different absolute numbers but basically kept the same ratings. The updated notebook is available on Github at the link provided, and the numbers are updated in the blog post.